
Uncovering the grammar of neural coding structures
An interview with Dr Eleonora Russo, Johannes Gutenberg University of Mainz (Germany), conducted by Hyewon Kim
Faced with the sheer number of neurons in the brain of any animal, it can be daunting to imagine how the combined activity of these cells gives rise to cognition and behaviour. In a recent SWC Seminar, Dr Elenora Russo shared her work investigating the coding structures the brain uses when engaged in different tasks. In this Q&A, she delves into how she became interested in researching this topic, the techniques used to understand the hidden regularities in neuronal dynamics, some implications of her findings, and more.
How much was already known about the way neuronal dynamics encode information and/or generate behaviour?
Historically, there have long been models of neuronal dynamics. For example, the concept of attractor models has been one of the most predominant and more influential in neuroscience. Attractor models assume that there are certain configurations of a neuronal network, which are not only favoured by the network and readily accessible, but that the network would spontaneously correct itself to return to these special configurations at any point in time in which the configuration is not the preferred one. These configurations are called ‘attractors’ because the network would spontaneously modify its activity until retrieving one of the preferred configurations, almost as if it would be attracted by them. Importantly, these are dynamical models because they tell you how the network activity evolves from one point in time to another.
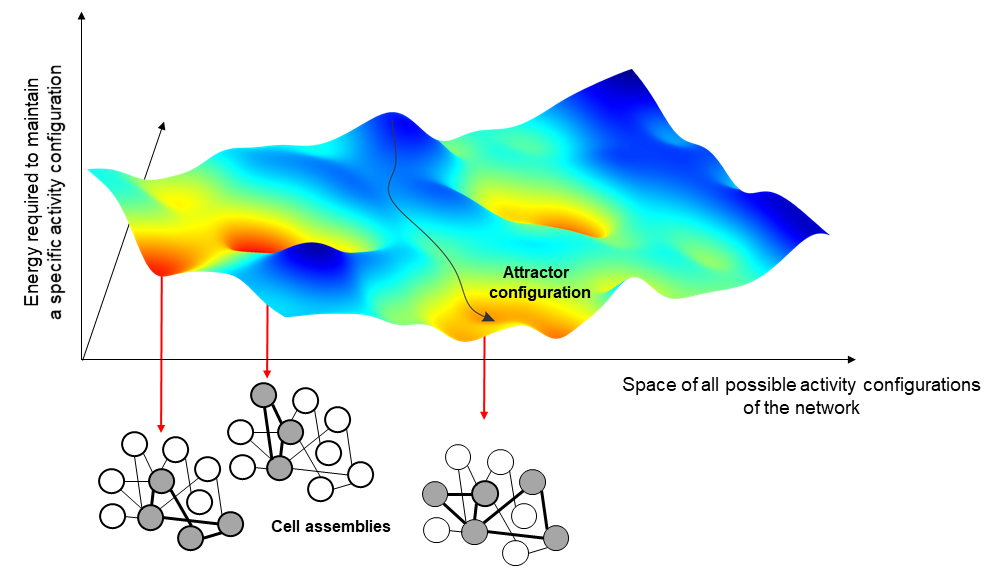
The variable strength of interaction between the neurons of a network leads to the formation of activity configurations that are particularly favored by the network, as less costly to maintain. In Hopfield models, these configurations go under the name of attractors and correspond to the activation of a selected group of neurons, the cell assemblies, particularly interconnected with each other.
To understand this concept, one can imagine that each possible network configurations correspond to a different point in a mountainous landscape and that different attractors correspond to the lowest point of different valleys. In this picture, the actual state of the network at a certain point in time would correspond to a ball that we let free to roll in this hilly landscape. We all know that if we let a ball fall, this will roll down until stopping at the very bottom of the valley. Thus, in the same way we can predict where the ball will pass and stop if we know the shape of the mountain and we assume gravity, we can predict the evolution of the neural activity if we can capture in our models the relation between the different activity configurations of the brain.
One of the most common applications of these kinds of models is to represent memories in our mind and to support generalisation. When we see a pen, for instance, we never in our lifetime see the same image of a pen twice because we always see it from a different perspective or angle; or, we might have never even seen that specific pen before. Still, we would be able to recognise it as a pen. This is called generalisability, and it is achieved by attractor neural networks with a similar mechanism as the one described before.
All these different images of pens activate in our brain different configurations of neural activity, which are not quite the same but are all somewhat related. We could say that they live in the same valley. When we recognise an image as ‘a pen’, what we do is to let the neural activity evolve until we spontaneously reach the attractor configuration corresponding to the concept of pen at bottom of the valley. This configuration is different for each one of us and has been shaped by all our subjective experiences. Interestingly, this configuration does not correspond to anything that we actually have ever experienced; in a way, it is some sort of abstract idea of a pen.
How did you become interested in researching this topic?
I’m a physicist and physicists love to simplify – maybe sometimes to an extreme! I always saw the brain as machinery that encodes some function that evolves in time in an organised way. I have always been curious about finding a simple way to generally describe the basic fundamental mechanisms at the basis of our thinking. An intriguing idea is that the same set of mechanisms could be present in different parts of the cortex, generating with the same set of tools different cognitive functions or different aspects of our mental processing. It’s like discovering the grammar of our neural coding. For example, a verb is a verb, although you can change the specific meaning carried by the verb, the verb will always have the same role in a sentence.
In a similar vein, I think there are some recurrent mechanisms in the brain, for example whenever there are oscillations or a certain connectivity structure between neurons, that favours certain dynamics. These dynamics might lead to a specific function, whose content would then be determined by a specific brain region. This is how I got interested in trying to find a kind of coding grammar in the dynamics of neural activity.
How does your research try to understand the hidden regularities in neuronal dynamics?
I use a variety of methodologies, which all try to leverage the same idea. As we live in a three-dimensional space, one can imagine the neuronal activity moving in a similar space, of however much higher dimension. If we consider a space with the same number of dimensions as the number of all neurons in the brain, then by using the activity of the neurons as a set of coordinates we can identify a point in the space representing the activity of the brain at a certain moment. As time evolves, this point will move in the space.

Activity of the medial prefrontal cortex of a rat while it is performing a spatial memory task. Black dots correspond to the prefrontal cortex activity at different moments in time. To allow visualisation, the high-dimensional activity space is here reduced to a three-dimensional space with dimensionality reduction techniques. As one can notice, particular activity configurations (correspondent to spots with a higher density of dots) occur more frequently than others.
The basic idea behind finding regularities in neural dynamics is that if we perform multiple times a cognitive function that involves a set of neurons, for multiple times we will cross the same point in the neural activity space. It’s like walking past the same point in a room, but only in an abstract space of neural activity. The idea is to capture places in this abstract space where the brain happens to return multiple times. If such places are there, then there must be something special about them. By collecting all the points that have been visited by our neuronal activity during the time in which the animal did something specific, one could see that there are locations that are more visited than others. Then, once we have identified such locations, we can understand to which cognitive function they correspond by looking at what the animal was doing in the collection of moments in which the neuronal activity was in those locations.
So, the whole idea is about determining which locations in this abstract neuronal activity space are more visited than others. To do this, there are many options, one of which is the detection of cell assemblies. Cell assembly detection finds sets of neurons, the cell assemblies, whose activation repeats in a stereotypical way multiple times during our experimental neuronal recordings. These patterns will correspond to those locations that are more visited than others in the neuronal activity space.
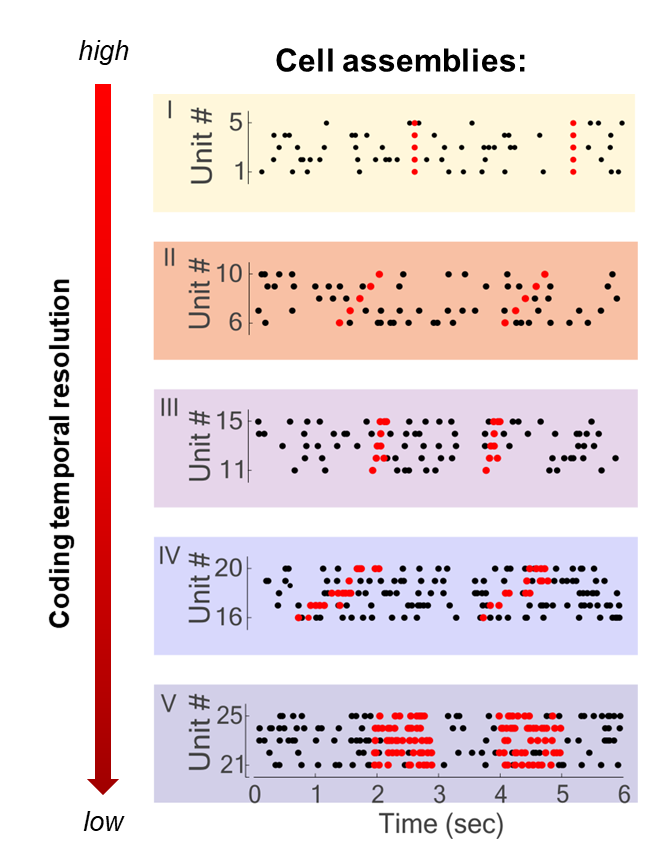
Five different assembly types composed of five units each, and with variable activity patterns and temporal resolution illustrated here on simulated data. Marked with black dots are the spike time of simulated neurons (units), in red the spike time of neurons when the assembly is active.
For example, we might find that a given pattern composed of three neurons firing at the same time and another neuron following by a few milliseconds occurs quite often and, importantly, not by chance. Since we see that such a pattern occurs more often than others, we can imagine that this pattern must have some meaning for the animal or, more generally, have a function. To understand this function, we have to look at when this pattern occurred and might figure out that the pattern is actually encoding the concept of, e.g., a pen. So every time we think about a pen, the same pattern will activate in some brain region. This is one technique, the detection of cell assemblies.
But there are also many more techniques, another being dynamical system reconstruction. On top of capturing the place that is more visited than others in this abstract neuronal space, dynamical system reconstruction also tells you how the system got there. Dynamical reconstruction captures the evolution of a brain region by making a mathematical model of the system (this is a simplified model, but it does reflect what is going on in the data). Dynamical system reconstruction aims to tell us why, after a certain configuration of the network, another set of configurations result. For example, it maybe tells us that these neurons that we record all get summed up and generate the activity at the next point in time of other neurons.
This is very useful information because we start to get into the mechanism of the neuronal activity of the brain. While cell assembly detection is more a descriptive technique, it tells us which relevant patterns are there, dynamical system reconstruction aims to tell us why certain patterns get activated and where we go next from there. Thus, we can actually make predictions about what is important to generate a physiological neuronal activity and simulate what could happen if this activity would be altered. Eventually, this might also be useful to investigate mental illnesses, as by looking at the differences in neural dynamics between healthy subjects versus patients, we can make some hypotheses about the emergence of some diseases. This is an emerging approach but I believe it will be very useful in the future.
What have been your key findings so far? Were you surprised by any of these findings?
Over the years I worked on the neuronal coding involved in several cognitive functions, ranging from decision-making to reinforcement learning. And each of these works of course tells a story. If I have to choose one of them then I can tell you about a finding regarding cell assemblies and how variable can the neural code be in different brain regions. You have to know that there is a long-standing debate in neuroscience about the precision at which information is encoded and transferred in the brain. One possibility is that information is carried by the exact timing of the spikes of the neurons. If this is true we should observe cell assemblies activity patterns composed of very precise constellations of single spikes.
This idea has however been antagonised by some neuroscientists. Let’s say we see an object. The image triggers activity in the neurons of the brain with a precise timing, exactly at the time of the visual input. As soon as the signal crosses the synapse to the next neuron, however, we come to face the fact that synaptic activity is stochastic. So, at every step of the information processing, you have to add some uncertainty in the timing. Some neuroscientists have therefore said that we cannot have a neural code based on such precise timing of neuronal activity, called temporal coding, but that we must have rate coding instead. Rate coding assumes that what carries information in the activity of a neuron is not the exact time of firing but the rate at which the neuron fires, that is the average number of spikes it produces in a specific period of time.
To investigate this fundamental question, with colleagues we developed a mathematical method that is not only able to detect the cell assemblies but is also able to tell us what is the temporal precision of their activity pattern. By using this method on neuronal recordings from different brain regions, we saw that both theories of neural coding are correct. But it depends on the brain region and the type of task that the animal was performing. This is because there are different processes in the brain, likely modulating the precision of the neurons’ firing rate, which are recruited when needed by different tasks. What we saw was that the same task could produce activity at different temporal scales and temporal patterns in different brain regions, but also that the same region might use different coding when engaged in different tasks. So, it’s important to keep in mind that both rate coding and temporal coding exist in the brain – it depends on the brain region and task.
What implications do your findings have for humans?
Animals and humans are not so different after all, so understanding how the information is encoded and which part of the complex mix of electrochemical processes constantly going on in our brain is actually relevant for the execution of a specific cognitive function is an important step in finding ways to help when these functions are impaired. Moreover, similar approaches based on the same fundamental ideas are already applied to human data coming from less invasive techniques such as fMRI or EEG. So we are already in the condition to study the neuronal dynamics of patients and healthy subjects.

About Dr Eleonora Russo
Eleonora Russo is an independent research fellow at the Johannes Gutenberg University of Mainz (Germany). She studied physics at the University of Pisa in Italy and received a PhD in Neuroscience from the International School for Advanced Studies (SISSA) in Trieste for her work on modelling free association dynamics in the cortex. She moved to Mannheim (Germany) as postdoctoral fellow at the Central Institute of Mental Health, where later became an Independent Research Fellow of the Chica and Heinz Foundation. Her research focuses on the investigation of cognitive processes by combining modelling with mining experimental data with statistical machine learning techniques.